深度学习入门：与学习相关的技巧

本文最后更新于 about 2 years ago，文中所描述的信息可能已发生改变。

施工中

内容参考：

• 《深度学习入门：基于 Python 的理论与实现》(斋藤康毅)
• 上述书籍作者提供的代码

参数的更新 ​

实际问题中参数空间可能非常复杂，很难快速找到最优解。

SGD ​

SGD 的策略很好理解，就是沿着梯度方向更新参数，寻找使损失函数值尽可能小的参数。可以写成如下式子：

$$\boldsymbol{W} \leftarrow \boldsymbol{W} - \eta \frac{\partial L}{\partial \boldsymbol{W}}$$

其中 $\boldsymbol{W}$ 表示要更新的权重参数，$\frac{\partial L}{\partial \boldsymbol{W}}$ 是损失函数关于 $\boldsymbol{W}$ 的梯度，$\eta$ 表示学习率（一般取0.1或0.01等事先确定的值）。

将 SGD 的方法用类的形式实现：

class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr  # 学习率

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

SGD 可以作为代码中的 optimizer 来进行参数更新。只要不同的最优化方法都实现 update(params, grads)，就可以用 optimizer.update(params, grads) 的形式在代码中完成更新参数的步骤。

从上面可以看出，SGD 的实现也很简单。然而在某些情况下（比如梯度并没有指向最小值的方向），SGD 的效率并不理想。例如，对于函数 $f(x, y) = \frac{1}{20} x^2 + y^2$，它的函数图形和等高线如图所示：

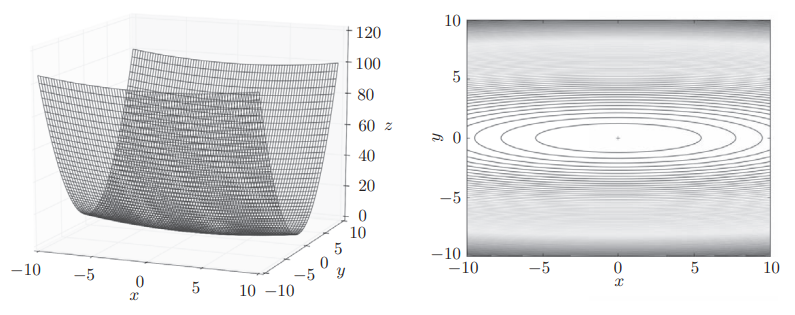
梯度如图所示：

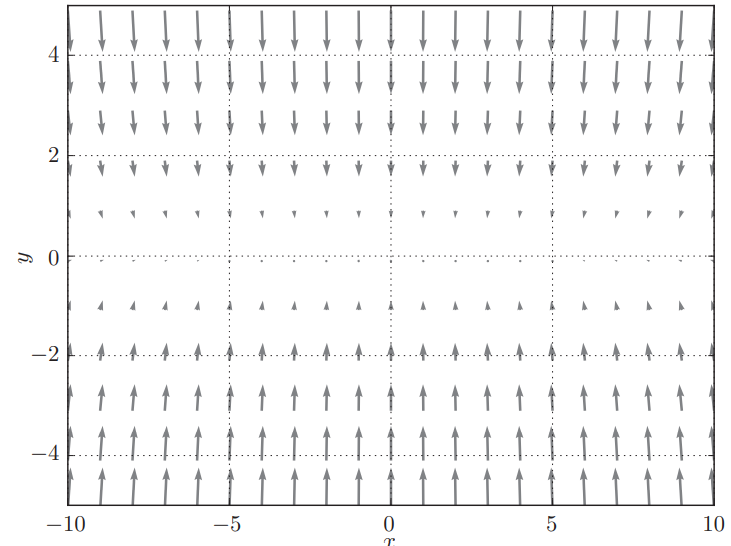
显然函数在 $(x, y) = (0, 0)$ 处取得最小值，但是在很多地方，梯度并不指向 $(0, 0)$。对这个函数使用 SGD，比方说从 $(x, y) = (-7.0, -2.0)$ 处开始搜索，更新路径会像这样：

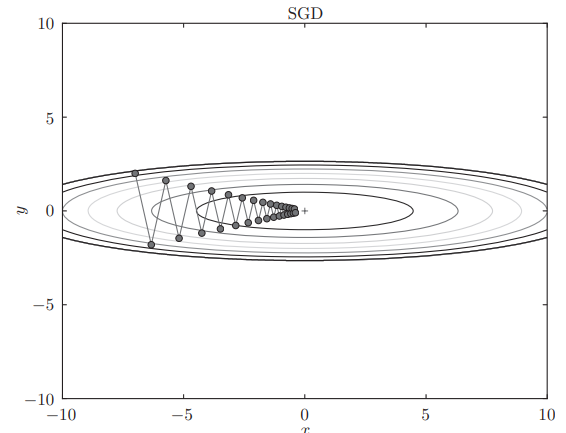
由于很多地方的梯度不指向 $(0, 0)$，这个更新路径呈“之”字形，显然不是很理想，效率不高。所以我们需要其他的更新方法。

Momentum ​

Momentum 方法引入了“速度”，“速度”的更新可以看作物体在梯度方向上受力：

$$\boldsymbol{v} \leftarrow \alpha \boldsymbol{v} - \eta \frac{\partial L}{\partial \boldsymbol{W}}$$

$$\boldsymbol{W} \leftarrow \boldsymbol{W} + \boldsymbol{v}$$

$\alpha \boldsymbol{v}$ 在物体不受力时会使速度衰减（$\alpha$ 一般取零点几的值），可以看作空气等带来的阻力。

Momentum 方法的代码实现：

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)  # “速度”的形状与参数相同

        for key in params.keys:
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]

对于之前的问题，Momentum 方法的更新路径：

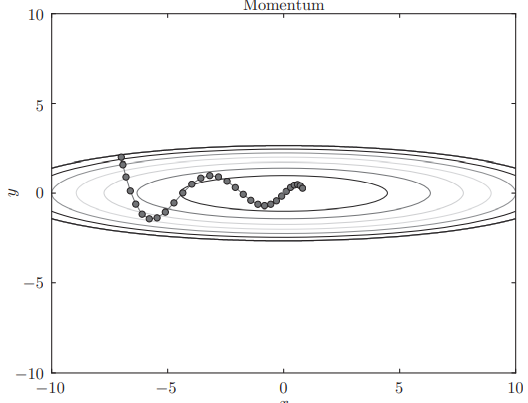
AdaGrad ​

AdaGrad 方法基于“学习率衰减”的想法：随着学习的进行，使学习率逐渐减小。实际上，AdaGrad 方法在学习过程中会为参数的每个元素调整学习率。

$$\boldsymbol{h} \leftarrow \boldsymbol{h} + \frac{\partial L}{\partial \boldsymbol{W}} \odot \frac{\partial L}{\partial \boldsymbol{W}}$$

$$\boldsymbol{W} \leftarrow \boldsymbol{W} - \eta \frac{1}{\sqrt{\boldsymbol{h}}} \frac{\partial L}{\partial \boldsymbol{W}}$$

$\odot$ 表示对应矩阵元素的乘法，$\boldsymbol{h}$ 表示以前所有梯度值的平方和。显然参数中变动较大的元素的学习率会变得更小（准确地说是学习率会被乘以一个更小的因数）。

实现过程：

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)  # 1e-7避免将0用作除数

这个方法在 $f(x, y)$ 中的更新路径：

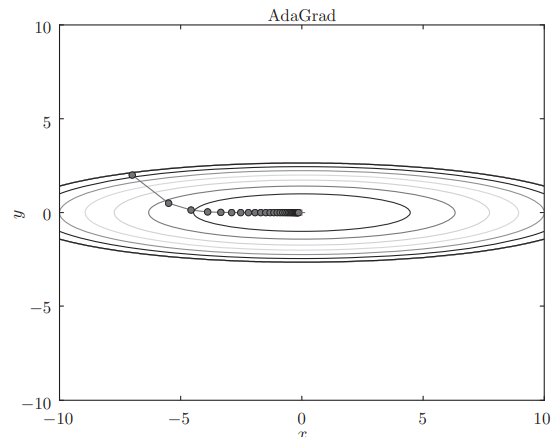
因为 y 方向的更新幅度较大，在这个方向上的学习率衰减也就更明显。

当然还有别的方法，比如融合了 Momentum 和 AdaGrad 的 Adam 方法，就不再说明了。（因为原书中也只给了相关论文和代码实现。）

使用不同的方法可以得到不同的更新路径，对于前面的问题来说 AdaGrad 能得到比较理想的路径，但如果换一个问题，可能其他方法会有更好的结果。（那是自然。）

权重的初始值 ​

初始值可以为0吗 ​

权值衰减是一种抑制过拟合的技巧，它以减小权重参数的值为目的进行学习。如果想减小权重，最好的方法是一开始就把权重设定为较小的值。那把权重的初始值设为0（说到更普遍的情况，其实是把权重初始值设置为一样的值）呢？

考虑误差反向传播就可以发现，将权重初始值设置为一样的值，反向传播时也会被更新为一样的值。都是一样的值的话神经网络为什么要有许多权重呢？

原来如此，所以必须随机生成初始值！

隐藏层的激活函数层的分布 ​

这里书上举的例子就不那么详细地复述了……

向一个5层神经网络传入随机生成的输入数据，激活函数使用 sigmoid 函数，权重使用标准差为1的高斯分布随机生成，用直方图绘制出各层激活值（激活函数的输出）的分布：

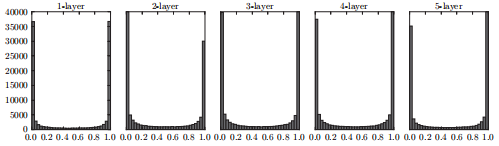
可以发现，各层的激活值都集中在0和1附近。对于 sigmoid 函数，在0和1附近的导数都比较接近0，那么这样的数据会造成反向传播中梯度的值不断变小，也就是所谓“梯度消失”

如果将权重的标准差设为0.01，各层的激活值分布就会变成：

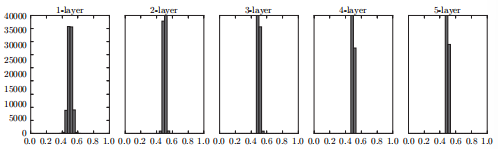
激活值集中在0.5附近，不会有梯度消失的问题，但是分布太过集中。显然不能让几乎所有的神经元都输出一样的值，实际应用中一般使用“Xavier 初始值”，可以避免这些问题。

Xavier 初始值控制权重尺度（标准差）的方式是：如果前一层的节点数为n，则初始值使用标准差为 $\frac{1}{\sqrt{n}}$ 的分布。

实现方式可以是：

pre_node_num = 100 # 前一层的节点数
w = np.random.randn(pre_node_num, node_num) / np.sqrt(pre_node_num)

使用 Xavier 初始值得到的各层激活值分布：

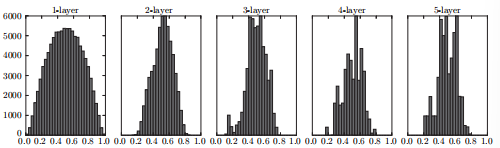
比之前的分布更有广度。

如果用 tanh 函数（双曲线函数）代替 sigmoid 函数，可以改善后面的层激活值歪斜的问题。

ReLU 的权重初始值 ​

Xavier 初始值是以激活函数是线性函数为前提而推导出来的。因为 sigmoid 函数和 tanh 函数左右对称，且中央附近可以视作线性函数，所以适合使用 Xavier 初始值。但当激活函数使用 ReLU 时，一般推荐使用 ReLU 专用的初始值，也就是 Kaiming He 等人推荐的初始值，也称为“He 初始值”。当前一层的节点数为 n 时，He 初始值使用标准差为 $\sqrt{\frac{2}{n}}$ 的高斯分布。当 Xavier 初始值是 $\sqrt{\frac{1}{n}}$ 时，（直观上）可以解释为，因为 ReLU 的负值区域的值为0，为了使它更有广度，所以需要2倍的系数。

用作者给出的 ch06/weight_init_compare.py 可以比较使用不同权重初始值时神经网络的学习情况。

Batch Normalization ​

前面调整权重的初始值是为了使各层的激活值分布有合适的广度，还有一种办法可以“强制性”地调整激活值的分布来达到这个目的。

Batch Norm 算法（前向传播） ​

Batch Norm有以下优点。

• 可以使学习快速进行（可以增大学习率）。
• 不那么依赖初始值（对于初始值不用那么神经质）。
• 抑制过拟合（降低Dropout等的必要性）。

Batch Norm 的思路是调整各层的激活值分布使其拥有适当的广度，为此需要在神经网络中插入对数据分布进行正规化的层（Batch Norm层）：

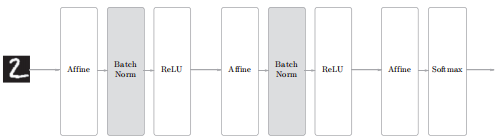
Batch Norm 是以学习时的 mini-batch 为单位，按 mini-batch 进行正规化，数学式表示：

$$\mu_B \leftarrow \frac{1}{m} \sum_{i = 1}^m x_i$$

$$\sigma_B^2 \leftarrow \frac{1}{m} \sum_{i = 1}^m (x_i - \mu_B)^2$$

$$\hat{x}_i \leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}$$

对 mini-batch 的 m 个输入数据的集合 $B = \{ x_1, x_2, ... , x_m \}$ 求均值和方差 。然后，对输入数据进行均值为0、方差为1（合适的分布）的正规化。其中 $\epsilon$ 是一个微小值。

Batch Norm 层会将正规化后的数据进行缩放和平移的变换：

$$y_i \leftarrow \gamma \hat{x}_i + \beta$$

一开始参数 $\gamma = 1$，$\beta = 0$，可以通过学习调整到合适的值。

正则化 ​

过拟合 ​