本文最后更新于 over 3 years ago,文中所描述的信息可能已发生改变。
内容参考:
- 《深度学习入门:基于 Python 的理论与实现》(斋藤康毅)
- 上述书籍作者提供的代码
之前成功实现了一个神经网络的学习过程,但是实际开始计算就会发现整个过程实在是太慢了……对所有参数都要计算梯度,而且要计算很多遍,显然我们需要一种能更快地计算出权重参数梯度的方法。
关于计算图
计算图能够将计算过程用图形(数据结构图,用多个节点和边表示)表示出来。
计算图与反向传播
使用计算图是为了直观理解反向传播法,那至少应该能先看懂计算图才行。
书上的例题1:太郎在超市买了2个100日元一个的苹果,消费税是10%,请计算支付金额。过程很简单,先算出2个苹果的价格,再算出加上消费税之后的花销。用图表示:

在这张图中,苹果单价流到“”节点,又被传递给“”节点,得出最后的价格。图中“”和“”是作为一个运算的整体,也可以只用 表示乘法,将“2”和“1.1”等作为变量标在外面:
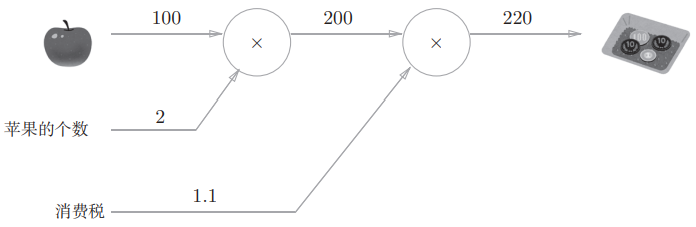
依此类推,其他问题也可以用这个方法表示,比方说太郎再买若干橘子,可以把橘子个数和单价传给乘法的节点,再把算出的橘子价格和苹果价格都传到一个加法节点,将总的价格拿去算消费税。用计算图解题的步骤可以归纳为:
- 构建计算图;
- 在计算图上从左到右进行计算。
上面“从左到右进行计算”的过程就是所谓正向传播,那么从图上从右向左就是反向传播。
局部计算与其他
尽管问题的全局可能非常复杂,但是计算图能够分节点将整个计算过程分解成简单的计算。
此外,可以借助计算图反向传播高效计算导数。比方说前面计算了购买2个苹果时加上消费税最终需要支付的金额,如果想知道道苹果价格的上涨会在多大程度上影响最终的支付金额(即支付金额关于苹果价格的导数),可以看这张图:
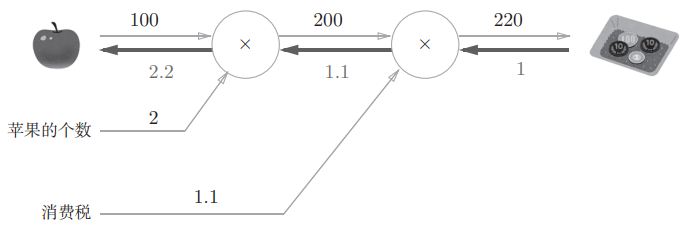
反向传播传递“局部导数”,在这个例子中反向传播从右向左传递导数的值(1、1.1、2.2),由此可知支付金额关于苹果价格的导数值是2.2。
使用这种方法,中间求得的导数结果可以被共享,从而提升计算效率。
链式法则
反向传播传递局部导数的原理是基于链式法则的,它如何对应计算图上的反向传播呢?
计算图的反向传播
假设有 ,它的反向传播:
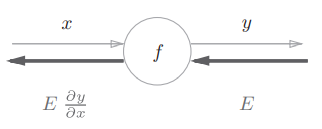
如图所示,反向传播的计算顺序是将上游传过来的值(信号 )乘以节点的局部导数(这里是 关于 的导数 )再传给下一个节点。
链式法则的原理
链式法则要先从复合函数说起,复合函数就是由多个函数构成的函数。例如 是由下面两个式子构成的:
链式法则的定义:如果某个函数由复合函数表示,则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。也就是说,对于上面的复合函数,有:
尝试使用链式法则求 ,有:
那么:
链式法则和计算图
用计算图表示上面的计算过程:
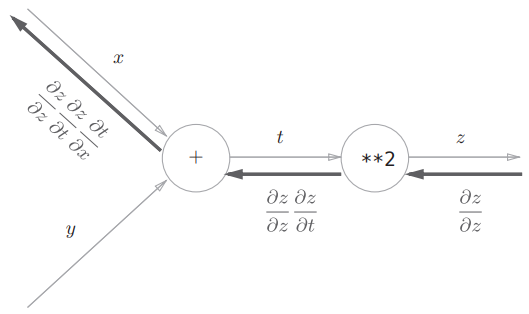
以“**2”节点为例,正向传播时输入为 ,输出为 ,所以局部导数为 ,反向传播时的输入为 (1),将其乘以局部导数再传给下一个节点。最终代入各个局部导数可以得到结果。
反向传播
加法节点的反向传播
以 为例,它的导数:
用计算图表示( 表示反向传播时上游传过来的导数):
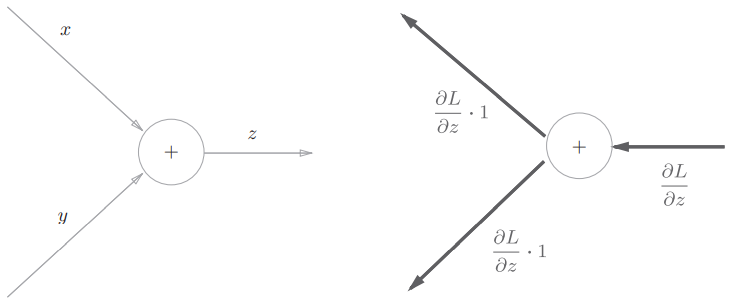
在本例中,因为 和 都是1,加法节点就是把上游传过来的导数乘以1再传给下一个节点。
乘法节点的反向传播
以 为例,它的导数:
画出计算图:
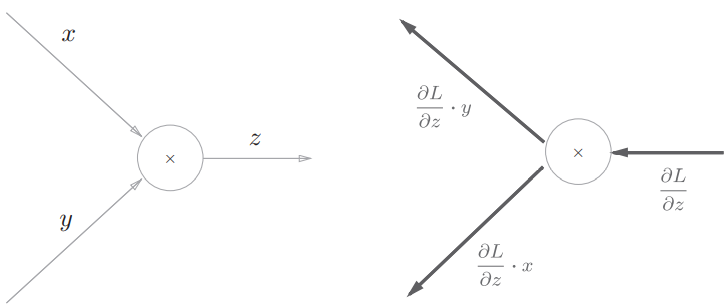
如果正向的时候信号是 ,反向的时候局部导数就是 ;正向的时候信号是 ,反向的时候局部导数就是 。表现为一种“翻转”的关系。乘法节点需要保留正向传播时传入的参数信息。
简单层的实现
知道了反向传播是怎么回事,不妨再来看看怎么用代码实现相关的乘法和加法节点(“层”)。
乘法层的实现
对于 ,有实现:
class MulLayer:
def __init__(self) -> None:
self.x = None
self.y = None
def forward(self, x, y):
self.x = x
self.y = y
out = x * y
return out
def backward(self, dout):
dx = dout * self.y # 翻转 x 和 y
dy = dout * self.x
return dx, dy用这个乘法层实现最开始说的买苹果的问题,计算图如下:
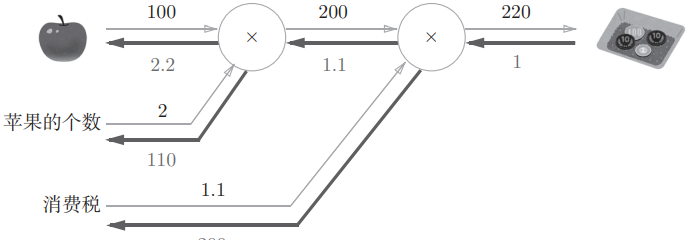
正向传播的计算过程:
apple = 100
apple_num = 2
tax = 1.1
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()
# 正向传播过程
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)
print(price) # 结果是220.00000000000003反向传播求过程中各个变量的导数:
# 反向传播过程
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)
print(dapple, dapple_num, dtax) # 结果是 2.2 110.00000000000001 200加法层的实现
对于 ,加法层有实现如下:
class AddLayer:
def __init__(self) -> None:
pass
def forward(self, x, y):
out = x + y
return out
def backward(self, dout):
dx = dout * 1
dy = dout * 1
return dx, dy要解决的问题是买2个苹果和3个橘子,计算图如下:
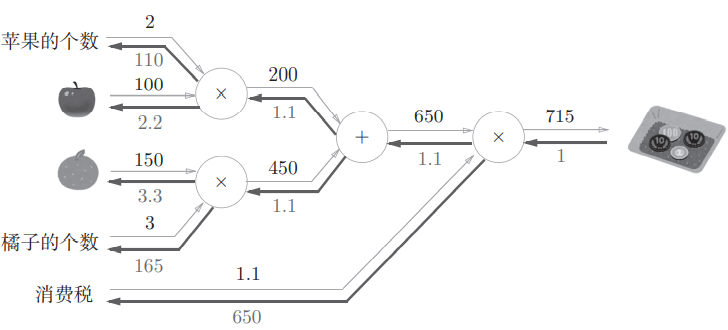
正向传播和反向传播的过程:
apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()
# 前向传播过程
apple_price = mul_apple_layer.forward(apple, apple_num) #(1)
orange_price = mul_orange_layer.forward(orange, orange_num) #(2)
all_price = add_apple_orange_layer.forward(apple_price, orange_price) #(3)
price = mul_tax_layer.forward(all_price, tax) #(4)
# 反向传播过程,要注意与正向传播的计算顺序相反
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice) #(4)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price) #(3)
dorange, dorange_num = mul_orange_layer.backward(dorange_price) #(2)
dapple, dapple_num = mul_apple_layer.backward(dapple_price) #(1)
print(price) # 结果是715.0000000000001
print(dapple_num, dapple, dorange, dorange_num,
dtax) # 结果是110.00000000000001 2.2 3.3000000000000003 165.0 650与计算图对照,显然能得到正确结果。
激活函数层的实现
既然简单的乘法加法等节点能用代码以层的形式实现,那么神经网络中的节点应该也可以,毕竟也没有复杂太多。把构成神经网络的层实现为一个类。先来实现激活函数的 ReLU 层和 Sigmoid 层。
ReLU 层
ReLU 函数:
关于 的导数:
那么,ReLU 层的计算图:
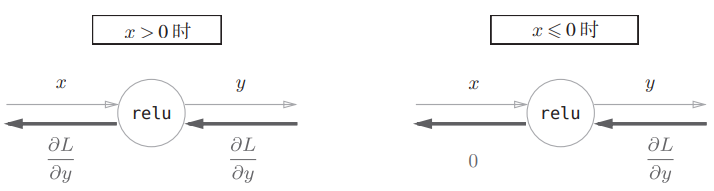
代码实现:
class Relu:
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x <= 0) # mask 是由 bool 值组成的 numpy 数组
out = x.copy()
out[self.mask] = 0 # 小于等于0的项置0
return out
def backward(self, dout):
dout[self.mask] = 0 # 正向传播时输入小于等于0的项对应导数是0
dx = dout
return dxSigmoid 层
Sigmoid 函数:
用计算图表示正向传播过程:
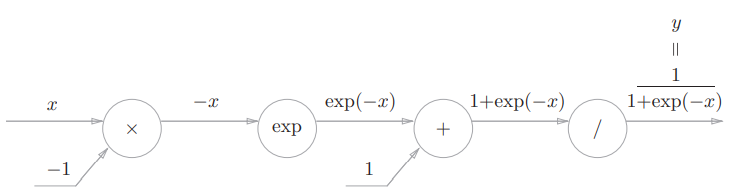
Sigmoid 函数的计算过程中出现了新的节点,需要看一看它们如何进行反向传播。
最后的“/”节点表示 ,它的导数可以解析性地表示为:
也就是说,反向传播时会将上游传过来的值乘以 ( 是正向传播时该节点的输出)再传给下游。
这个加法节点反向传播时显然是将上游传过来的值直接传过去。
“exp” 节点表示 ,导数如下:
正向传播时传入的是 ,反向传播时就把上游传过来的值乘以 再传给下游。
乘法节点是 与 相乘,所以反向传播时传给 方向的应该是上游的值乘以 。
包含反向传播的计算图如下:

由图可知反向传播的输出是 ,只根据正向传播的输入 和输出 就能得出,所以计算图可以简化:
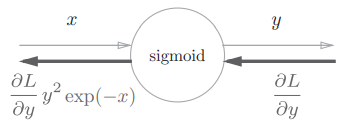
又因为 , 可以被简化为:
也就是说,Sigmoid 层的反向传播的输出,根据它正向传播时的输出就能算出来。
Sigmoid 层的代码实现:
class Sigmoid:
def __init__(self):
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out # 根据正向传播的输出计算反向传播的结果
return dxAffine/Softmax 层
Affine 层进行仿射变换,也就是矩阵乘积?(实际上还要算上与偏置之和?)
用层的方式实现矩阵乘积和 Softmax 节点。
Affine 层
矩阵相乘时对应维度的元素个数必须一致,比如:

求加权信号的和包括计算矩阵乘积以及与偏置求和。用计算图表示这些运算,其中用“dot”节点表示矩阵乘积:
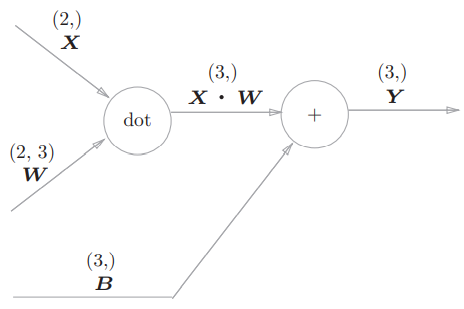
各个节点间传播的是矩阵。
考虑上图“dot”节点的反向传播,有:
那么上面计算图的反向传播:

如果输入数据不是单个数据而是批,反向传播时矩阵形状会有所不同:
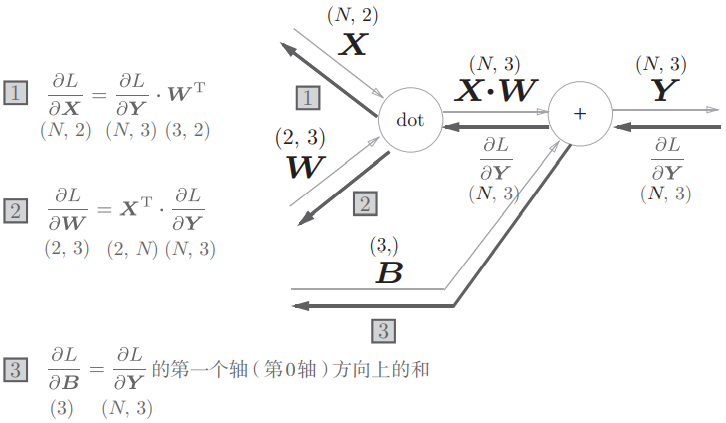
一种代码实现:
class Affine:
def __init__(self, W, b):
self.W = W
self.b = b
self.x = None
self.dW = None
self.db = None
def forward(self, x):
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dxSoftmax-with-loss 层
最后是输出层的 softmax 函数,考虑作为损失函数的交叉熵误差。
假设要进行3类分类,从前面的层接收3个输入。Softmax 层将输入 正规化,输出 。Cross Entropy Error 层接收 Softmax 的输出和监督数据 ,输出损失 。简化后的计算图:
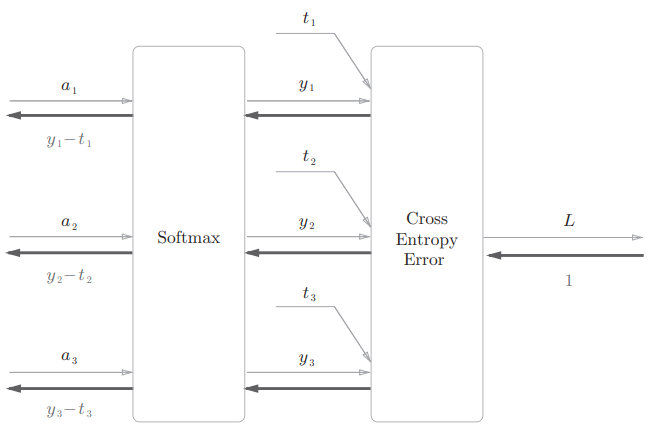
实现过程:
class SoftmaxWithLoss:
def __init__(self):
self.loss = None # 损失
self.y = None # softmax 的输出
self.t = None # 监督数据(one-hot vector)
def forward(self, x, t):
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = (self.y - self.t) / batch_size # 单个数据的误差
return dx误差反向传播法的实现
已经知道神经网络学习的步骤如下:
- 前提
- 神经网络存在合适的权重和偏置,调整权重和偏置以便拟合训练数据的过程称为“学习”。神经网络的学习分成下面4个步骤。
- 步骤1(mini-batch)
- 从训练数据中随机选出一部分数据。
- 步骤2(计算梯度)
- 求出各个权重参数的梯度。
- 步骤3(更新参数)
- 将权重参数沿梯度方向进行微小更新。
- 步骤4(重复)
- 重复步骤1、步骤2、步骤3
误差反向传播法在第二步中出现。之前计算梯度是通过数值微分求的,实现简单,不过计算起来要花费比较长的时间,用误差反向传播法可以改善这一点。
我们已经将网络中的节点表示成了“层”,网络获取结果和计算梯度的过程可以由层之间的传递完成。对应误差反向传播法的2层网络的实现:
import sys, os
sys.path.append(os.curdir)
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict # 有序字典
class TwoLayerNet:
def __init__(self,
input_size,
hidden_size,
output_size,
weight_init_std=0.01) -> None:
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(
input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(
hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['ReLU'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t) # 算出交叉熵误差
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1:
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
# 对每层的参数求梯度
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
def gradient(self, x, t):
# 前向传播
self.loss(x, t)
# 反向
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads误差反向传播法的梯度确认
像上面这样通过反向传播,使用解析性的方法计算梯度,虽然免去了数值微分的大量计算,但是实现比较复杂(各层分别实现,都不能出错),还是需要经常比较数值微分的结果和误差反向传播法的结果,以确认误差反向传播法的结果是否正确。这个“确认”的操作就是梯度确认。
实现如下:
import sys, os
sys.path.append(os.curdir)
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True,
one_hot_label=True)
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
x_batch = x_train[:3]
t_batch = t_train[:3]
grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)
# 每个权重梯度的绝对误差平均值
for key in grad_numerical.keys():
diff = np.average(np.abs(grad_backprop[key] - grad_numerical[key]))
print(key + ':' + str(diff))只要 diff 的值是一个接近0的很小的值就说明误差反向传播法的计算没有错误。
使用误差反向传播法的学习
与上一篇里的方法相比,不同之处就在于使用误差反向传播法来求梯度。实现如下:
import sys, os
import numpy as np
import matplotlib.pyplot as plt
sys.path.append(os.curdir)
from two_layer_net import TwoLayerNet
from dataset.mnist import load_mnist
# print('Load mnist dataset...')
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True,
one_hot_label=True)
# print('Initialize network...')
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 超参数
iters_num = 10000 # 梯度法更新次数
train_size = x_train.shape[0] # 训练集大小
batch_size = 100 # batch 大小
learning_rate = 0.1 # 学习率
train_loss_list = []
train_acc_list = []
test_acc_list = []
# 平均每个 epoch 的重复次数
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
# 获取 mini-batch
# print(i, ': choose mini-batch...')
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 计算梯度
# print(i, ': calculate grads...')
# grad = network.numerical_gradient(x_batch, t_batch)
grad = network.gradient(x_batch, t_batch) # 误差反向传播法
# 更新参数
# print(i, ': update params...')
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 记录学习过程
loss = network.loss(x_batch, t_batch)
# print(i, 'loss: ', loss)
train_loss_list.append(loss)
# 每个 epoch 完成后计算识别精度
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print('Train acc, test acc | ' + str(train_acc) + ', ' + str(test_acc))
# 画出图像
# markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list)) # 生成 x 坐标
plt.plot(x, train_acc_list, label='train acc') # 训练集识别精度
plt.plot(x, test_acc_list, label='test acc', linestyle='--') # 测试集识别精度,虚线
plt.xlabel("epochs") # 横轴单位
plt.ylabel("accuracy") # 纵轴单位
plt.ylim(0, 1.0)
plt.legend(loc='lower right') # 右下角图例
plt.show()效果立竿见影,比之前的快了不是一点半点。那就这样~