深度学习入门：感知机

本文最后更新于 about 2 years ago，文中所描述的信息可能已发生改变。

内容参考：

• 《深度学习入门：基于 Python 的理论与实现》(斋藤康毅)

感知机 ​

感知机（指“人工神经元”或“朴素感知机”）接收多个输入信号，输出一个信号。感知机的信号只有1和0两种取值。信号与权重的乘积之和超过阈值 $\theta$ 时神经元被激活。

有两个输入的感知机：

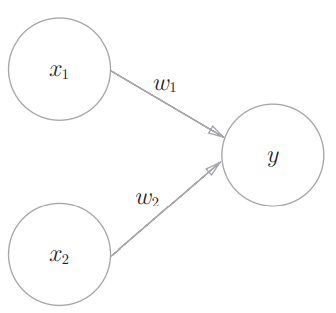
用数学式可以表示为：

$$y = \begin{cases} 0 & (w_1 x_1 + w_2 x_2 \le \theta) \\\ 1 & (w_1 x_1 + w_2 x_2 \gt \theta) \end{cases}$$

用感知机表示逻辑电路 ​

就拿与门举例吧，与门的真值表：

调整权重和阈值就可以满足表中的条件，例如当 $(w_1, w_2, \theta) = (0.5, 0.5, 0.7)$ 时，感知机就可以表示与门。

代码实现：

def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7 # 权重和阈值
    tmp = x1*w1 + x2*w2
    if tmp <= theta:
        return 0
    else:
        return 1

这是最直接的实现，为了“以后的事情”（书中原话，具体是为了什么，我得往后学再说），引入偏置 $b$，将 $\theta$ 换成 $-b$，感知机会计算信号和权重的乘积，再加上偏置。那么有两个输入的感知机可以表示为：

$$y = \begin{cases} 0 & (b + w_1 x_1 + w_2 x_2 \le 0) \\\ 1 & (b + w_1 x_1 + w_2 x_2 \gt 0) \end{cases}$$

利用 numpy 数组，用偏置和权重实现与门：

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    temp = np.sum(w*x) + b
    if temp <= 0:
        return 0
    else:
        return 1

显然权重可以衡量信号的重要性，偏置反映了神经元被激活（输出为1）的容易程度。

通过尝试可以发现，调整权重和偏置，可以用几乎一样的代码实现与非门和或门，但是无法实现异或门。为什么？

感知机的局限性 ​

举一个例子，权重参数为 $(b, w_1, w_2) = (-0.5, 1.0, 1.0)$ 时，感知机可以实现或门的逻辑。此时感知机会生成由直线 $-0.5 + x_1 + x_2 = 0$ 分割开的两个空间，一个空间输出1,另一个空间输出0。如图所示：

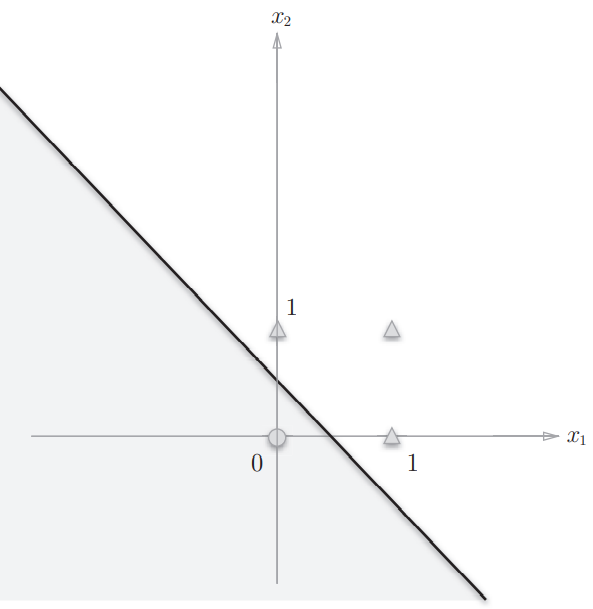
或门在 $(x_1, x_2) = (0, 0)$ 时输出0，在 $(x_1, x_2)$ 为 $(0, 1)$、$(1, 0)$、$(1, 1)$ 时输出1。图中 $\circ$ 表示输出0， $\triangle$ 表示输出1，感知机能做出一条直线将 $\circ$ 和 $\triangle$ 分开。与门和与非门的情况与之类似。

而异或门的输出空间如图：

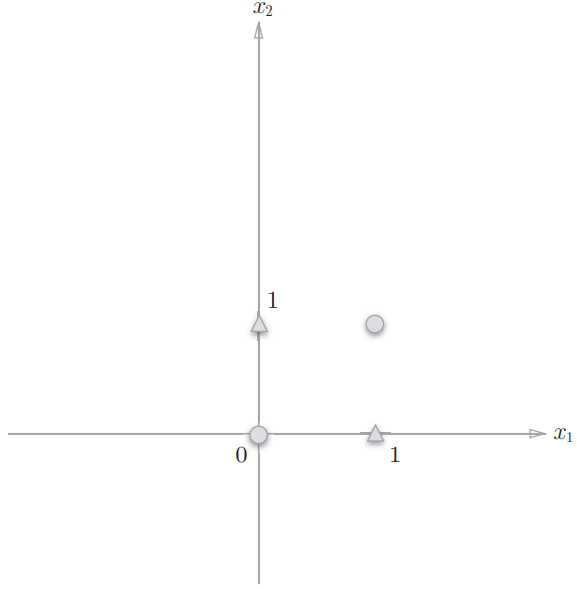
显然无法用一条直线将 $\circ$ 和 $\triangle$ 分开（不信可以多试试🤪），而感知机只能表示由一条直线分割的空间（线性空间，而上图这样由曲线分割的空间被称作非线性空间），所以就无法用感知机直接实现异或门（无法表示非线性空间）。

多层感知机 ​

但是实现异或门的方法很多，其中之一就是组合与门、与非门和或门，如图所示：

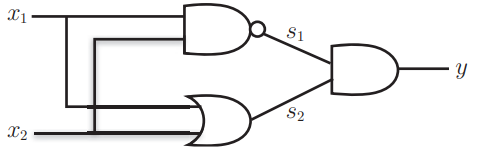
用 python 实现上图所示的异或门（假设已经实现了与门、与非门和或门）：

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

这里我们就成功用多个感知机实现了异或门，做到了之前做不到的事！可以用感知机的表示方法来表示这个异或门：

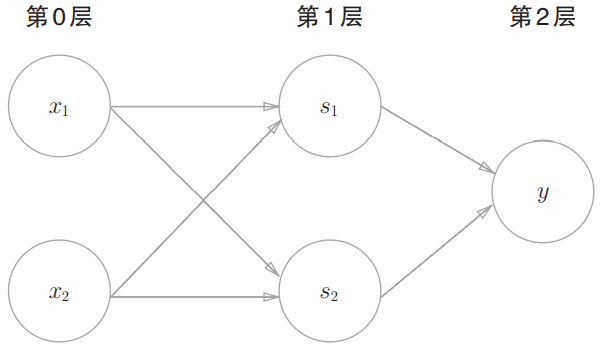
这个感知机与前面代表与门等逻辑门的感知机不同。实际上，与门、或门等是单层感知机，而异或门是2层感知机（只有两层有权重，可以看作简单的神经网络）。

1. 第0层的两个神经元接收输入信号，并将信号发送至第1层的神经元。
2. 第1层的神经元将信号发送至第2层的神经元，第2层的神经元输出 $y$。

从上面这一部分能看出什么呢？叠加感知机的层数就可以更灵活地表示更复杂的东西，比如表示非线性空间，甚至可以作为神经网络的基础。通过一些相关的图解可以发现，神经网络中神经元的连接方式和感知机应该是一致的。

PS：在这一点上，感知机和它能直接表示的那些最简单的逻辑门很像，都能作为更复杂逻辑结构的基本单位。

感知机和神经网络？且听下回分解……